从这一章开始，我们将学习三角学，并在第五章开始应用到动画技术中，其实在下一章的绘图技术中就会接触到。如果你已经对三角学有所了解或渴望学习动画方面的知识，那么可以跳过开始这部分，待日后遇到不懂的问题时，再回来学习。我们用到的90％的三角学都需要 Math.sin 和 Math.cos 这两个函数。在我写本书的第一版时，曾说过，除了在中学学习过的那些代数和几何外(而且由于时间久远大多都记不清了)，我没有接受过正规的数学培训，最初在本章中的内容都是来自于各种书籍，网站或是其它网络资源，这是因为这部分知识并不难，既然我能够学会，那么你也一定可以的。而现在我已经完成了大学代数和微积分课程，对于三角学也有了更为全面和系统的了解。我可以很荣幸地说，这一章的内容非常好，因为对于这个学科有了更为深入的了解，所以很多地方可以解释得更为清楚。

什么是三角学(Trigonometry)

三角学是一门研究三角形与其边和角关系的学科。当我们观察一个三角形时，发现它有三条边和三个角（因此称为三角），而且在这些边和角之间存在着一些特殊的关系。例如，增大其中的任何一个角，那么该角所对应的边就会增长（假设其它两条边长度不变），同时，其它两个角会变小，实际上，究竟它们变化了多少，加以计算后就可以得出一个比例。在一个三角形中，如果其中有一个角为90度，那么就称为直角三角形，并在该角的夹角处标出一个正方形（垂足），只有在直角三角形才会这样。学习直角三角形中存在的关系要比推导基本公式简单得多，这使得直角三角形成为一种非常有用的结构，本章及该书后面的内容大多都是直角三角形。

角(Angle)

角是三角学最主要的研究对象，让我们先来解决这个问题。角是由两条相交线构成的图形，或是两条相交线之间的那部分空间，空间远大，夹角越大。事实上，两条相交的线会形成四个角，见图 3-1：

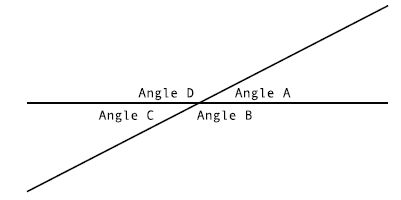
图3-1 两条线形成四个角

弧度制(radian)与角度制(degress)

弧度制与角度制是角度测量中的两种特殊制度。我们大概对于角度制最为熟悉，甚至闭着眼都能画出45度或90度的角。圆的360度体系已经成为了一种文化，人们常说“180度转弯”就是指“转到相反的方向”，这里并不是指转弯的方向，而是指一种相反的观点。我们所讨论的角度，对于计算机来说，就是弧度。所以，不管你是否喜欢，都要对弧度制有所了解。

1弧度约等于57.2958度。你也许会问“这符合逻辑吗？”确实有其逻辑所在。一个圆，360度，计算出的弧度为6.2832。仍然没有任何意义？好，想一下圆周率派 Pi(π) 约等于 3.1416，而一个圆(6.2832弧度)就等于2 pi。我们知道 360 度相当于 2 pi，180 度相当于 pi，90 度相当于 pi/2，等等。图3-2 给出一些常用的弧度制。

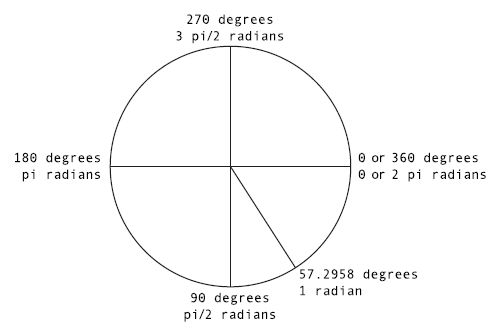
图3-2 弧度与角度

从现在起我们就要开始使用弧度制了，而且今后会遇到很多用弧度表示度的情况。

影片剪辑和 Sprite 影片的 rotation 属性都要使用角度制，而且属性非常会经常使用。例如，一辆汽车需要旋转到运动的方向，如果使用三角学计算运动方向，那么所得到的角度是以弧度制表示的，而汽车的旋转则需要使用角度制。相反，如果要指定某个对象向某个方向前进，就要获得它的旋转(rotation)角度，而这是用角度制表示的，如果要在三角函数中使用它就一定要转换为弧度制。
角度制，还应用在滤镜上，如果使用投影滤镜(drop shadow filter)，来为物体投射45度的阴影，就需要指定其角度而非弧度，不论是在 Flash IED 中还是使用 ActionScript 代码都一样。

为什么在一个编程体系里有两种截然不同的制度呢？也许这就是Flash双重性。一方面，这是设计人员的工具，在 Flash IDE 中拥有所有的绘图和变形工具，可以绘制出漂亮的图形。如果你对一名设计员说把你制作的 logo 文字旋转一个弧度，你肯定会遭白眼。另一方面，Flash 也是一个开发工具，更像一种编程语言，ActionScript 用户使用弧度制。总之，不论你是否喜欢都要使用到它们，而且还需要掌握角度制与弧度制间的相互转换。以下是公式：
弧度(radians) = 角度(degrees) * Math.PI /180
角度(degrees) = 弧度(radians) * 180 / Math.PI

在学习本书的过程中，会遇到很多公式。无论哪里，遇到需要记忆的公式时，我都会指出来，希望大家能够识记，这里是第一个公式。每次需要用到这些公式时，可以查找一下，但不会得到现成的代码，因为这些代码都需要用手敲进去。我使用 ActionScript 写这些公式，比如使用 Math.PI 要比使用 pi 或其它字符要好，因为这和我们输入的代码是一致的。

180度大约等于3.14…弧度。换句话讲，半圆为 pi 个弧度，整圆为 2 pi个弧度，一个弧度大概为 57.29…度。

出处：蓝色理想
责任编辑：bluehearts

上一页 下一页 三角学应用 [2]

◎进入论坛RIA设计与应用版块参加讨论