波形

大家肯定听说过正弦波，也一定见过图3-17所示的图形。

图3-17 正弦波形

那么为什么要把正弦函数与正弦图像两个不相干的东西联系到一起呢？如果将0到360度(或着0到2pi)代入到正弦函数中，那么就会得到这个正弦函数图像。从左到右代表所使用的角度值，而图中y坐标变化，代表这些角的正弦值。

图3-18中，标出了一些特殊的角度，我们可以看到0度的正弦值为0，90度或pi/2的正弦值为1，180度或pi的正弦值又回到0，270度或3/2pi的正弦值为-1，360度的正弦值为0。下面用 Flash 来试一下正弦波形，把以下代码放入文档类的框架中进行测试：

for (var angle:Number = 0; angle < Math.PI * 2; angle += .1) {
 trace(Math.sin(angle));
}

从现在起，要开始习惯只使用弧度制。除了使用 rotation 或其它只使用角度制的属性外，要开始学着不去使用角度制。

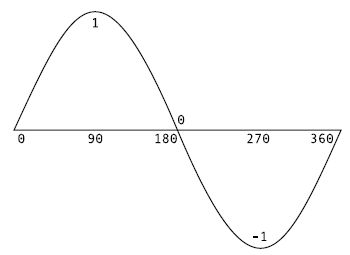
图3-18 正弦图像值

在这个例子中，角度从0开始，每次递增0.1直到大于 Math.PI*2 为止，并输出该角的正弦值。看一下输出结果，我们发现角度是从0开始，增加到1后，开始减小，减少到-1时，再回归至0。这些值不会真正准确地到达1或0，因为每次增加0.1，所以永远不会得到pi或pi/2的整数倍。

平滑的上下运动

如何使用 Math.sin(angle) 呢？如果想让物体上下或左右移动，那么就要用到这个函数。考虑：使用 0～1～-1～0 的变化来实现这个动画，并且反复地使用这个波形。

活动域仅仅是从1到-1，不能看出效果，所以要把这些数值放大一些，比如扩大100倍。这样就拥有了一个从100到-100的波形，并且连绵不断。在下面这个文档类 Bobbing.as 中，要使用一个在 Ball 类中定义的 Sprite 影片，请看代码：

package {
 import flash.display.Sprite;
 public class Ball extends Sprite {
  private var radius:Number;
  private var color:uint;
  public function Ball(radius:Number=40, color:uint=0xff0000) {
   this.radius = radius;
   this.color = color;
   init();
  }
  public function init():void {
   graphics.beginFill(color);
   graphics.drawCircle(0, 0, radius);
   graphics.endFill();
  }
 }
}

当这个类被实例化后，就能绘制出一个圆。我们还可以自行给出圆的半径(radius)和颜色(color)。如果不给这些参数的话，就会使用默认的参数：半径为40，颜色为红色（这是AS3.0新增的功能）。这个类非常简单，但却非常有用，今后在书中会经常用到，所以大家一定要掌握。

文档类创建一个 Ball 类的实例，并加入到舞台上，再为它增加一个 enterFrame 侦听器，这样就可以让小球上下移动了。

package {
 import flash.display.Sprite;
 import flash.events.Event;
 public class Bobbing extends Sprite {
  private var ball:Ball;
  private var angle:Number = 0;
  public function Bobbing() {
   init();
  }
  private function init():void {
   ball = new Ball();
   addChild(ball);
   ball.x = stage.stageWidth / 2;
   addEventListener(Event.ENTER_FRAME, onEnterFrame);
  }
  public function onEnterFrame(event:Event):void {
   ball.y = stage.stageHeight / 2 + Math.sin(angle) * 50;
   angle += .1;
  }
 }
}

首先，需要一个角度属性(angle)初始值为0。在 onEnterFrame 方法中，使用该角的正弦值并扩大50倍。这样一来，取值的范围就变成了50到-50。再在这个值上加舞台高度的一半，数值就变为从250到150(设舞台高度为400像素)，用这个值作为小球的Y坐标，最后为下一次循环增加0.1个弧度，这样就完成了小球平滑的上下运动。每一次循环的值都不相同，我们发现如果将0.1变为另一个数值的话，就改变了小球运动的速度。角度(angle)变化的快慢与 Math.sin 从1到-1变化的速度成正比。很明显，改变50这个值，就改变了小球移动的距离，而改变 stage.stageHeight / 2 的值，就改变了小球运动时围绕的位置。我们还可以给出一些抽象的值作为变量，代码如下(只给出需要改变或增加的部分)：

// at the top of the class:
private var angle:Number = 0;
private var centerY:Number = 200;
private var range:Number = 50;
private var speed:Number = 0.1;
// and the handler function:
public function onEnterFrame(event:Event):void {
 ball.y = centerY + Math.sin(angle) * range;
 angle += speed;
}

在运动代码中没有使用具体的数值，真是次非常好的练习，以后应尽量这样做。

出处：蓝色理想
责任编辑：bluehearts

上一页 三角学应用 [5] 下一页 三角学应用 [7]

◎进入论坛RIA设计与应用版块参加讨论