椭圆运动

想要获得一个椭圆该怎么办呢，其实很简单，问题就在于半径。如果让x和y运动的大小相同，那么就得到一个圆。如果想得到一个椭圆形，我们只需要在计算x和y位置时使用不同的半径值： radiusX 和 radiusY 。从严格的几何观点来看，使用这两个名称实在不怎么好，但是它们确实非常简单易懂，也非常好记非常直观，所以我还是坚持使用这两个变量名。下面看看它们是如何配合的，见 Oval.as：

package {
 import flash.display.Sprite;
 import flash.events.Event;
 public class Oval extends Sprite {
  private var ball:Ball;
  private var angle:Number = 0;
  private var centerX:Number = 200;
  private var centerY:Number = 200;
  private var radiusX:Number = 200;
  private var radiusY:Number = 100;
  private var speed:Number = .1;
  public function Oval() {
   init();
  }
  private function init():void {
   ball = new Ball();
   addChild(ball);
   ball.x = 0;
   addEventListener(Event.ENTER_FRAME, onEnterFrame);
  }
  public function onEnterFrame(event:Event):void {
   ball.x = centerX + Math.cos(angle) * radiusX;
   ball.y = centerY + Math.sin(angle) * radiusY;
   angle += speed;
  }
 }
}

这里， radiusX 为200，意味着小球在距离 centerX 200个像素内左右运动。 radiusY 为100，意味着小球上下运动的范围只有100像素，这样就得到了一个不匀称的圆。

勾股定理

最后，介绍一下勾股定理。虽然并不能算是三角学中正式的一部分，但是它与我们这个学科还是有一些关系的，并且还涉及到一个将来会经常使用的公式，所以在这里介绍它非常合适。

勾股定理是很久以前一个希腊人发明。这个定理是说 A的平方 + B的平方 = C的平方 ，听起来好像是儿歌，如果大家之前学过这个定理，那么交流起来效果最好。

深入探讨一下，另一种对该定理的叙述是：直角三角形的两条直角边的平方和等于斜边的平方，这句话真正说到点子上了。请看图3-21所示直角三角形。
两条直角边A和B长度为3和4，斜边C长度为5。毕达哥拉斯(Pythagoras)先生告诉我们 A2 + B2 = C2 。加入一些数字来检验一下，32 + 42 = 52，计算出 9 + 16 = 25。是的，非常正确。

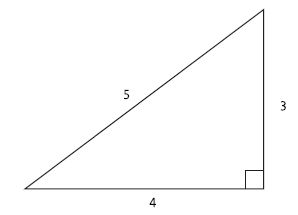
图3-21 一个直角三角形

如果大家已经知道了这个口决，那么勾股定理只不过就是一种有趣的关系。如果中知道其中两条边的长度，那么勾股定理就派上用场了，可以用它很快地求出第三条边的长度。在 Flash 中，最常见的情况是我们只知道两条直角边的长度要求出斜边的长度。比如，求出两点间的距离。

两点间距离

假设在舞台上有两个 Sprite 影片，想要求出它们之间的距离。这是勾股定理在 Flash 中最为常见的应用。那么如何实现呢？已知两个 Sprite 的 x,y 坐标，把第一个影片的位置称为x1,y1，另一个影片的位置称为 x2,y2，见图3-22。

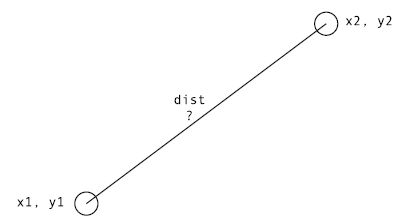
图3-22 两个物体间的距离是多少？

如果你在本章中看了太多的直角三角形，那么很容易就把图3-22看成一个直角三角形，而那条距离线(distance)就是三角形的斜边。在图3-23中，加入了这个三角形并填入了数字。

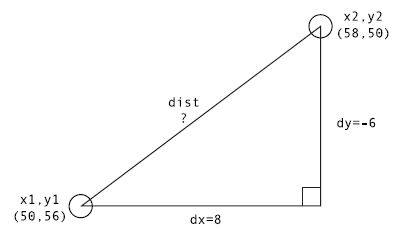
图3-23 变成一个直角三角形

dx为两个影片之间的x轴，dy为它们之间的y轴。用x2减x1就得到了dx的值：58 – 50 = 8，同样，用y2-y1等于6得到dy的值。现在使用勾股定理，将dx,dy的平方相加，就得到了距离(distance)的平方。

换言之，62 + 82 = dist2，相当于 36 + 64(=100) = dist2。基础代数学讲过可以通过开平方把它转化为 = dist。这样一来，就可以得出两个影片之间的距离为 10。

现在，把它抽像成一个公式，这样的话，今后再遇到同样的问题，就可以直接使用这个公式了。有两个位置 x1,y1 和 x2,y2，先计算出 x 的距离和 y 的距离，然后求出它们的平方和，最后求出平方根，下面请看 ActionScript 写法：

dx = x2 – x1;
dy = y2 – y1;
dist = Math.sqrt(dx*dx + dy*dy);

请特别注意这些代码，它们将是我们工具箱中又一个最好的工具。前两句是获得x,y轴上的距离。最后一句分为三个步骤：计算每个值的平方，把它们相加，求出平方根。下面进行一下实践，文档类 Distance.as ，创建了两个 Sprite 影片，并随机摆放，最后计算出它们之间的距离。

package {
 import flash.display.Sprite;
 public class Distance extends Sprite {
  public function Distance() {
   init();
  }
  private function init():void {
   var sprite1:Sprite = new Sprite();
   addChild(sprite1);
   sprite1.graphics.beginFill(0x000000);
   sprite1.graphics.drawRect(-2, -2, 4, 4);
   sprite1.graphics.endFill();
   sprite1.x = Math.random() * stage.stageWidth;
   sprite1.y = Math.random() * stage.stageHeight;
   var sprite2:Sprite = new Sprite();
   addChild(sprite2);
   sprite2.graphics.beginFill(0xff0000);
   sprite2.graphics.drawRect(-2, -2, 4, 4);
   sprite2.graphics.endFill();
   sprite2.x = Math.random() * stage.stageWidth;
   sprite2.y = Math.random() * stage.stageHeight;
   var dx:Number = sprite1.x - sprite2.x;
   var dy:Number = sprite1.y - sprite2.y;
   var dist:Number = Math.sqrt(dx * dx + dy * dy);
   trace(dist);
  }
 }
}

编译执行这个动画后，就得到了两个影片之间的距离。每次执行，两个影片的位置都会不同。不论它们处于什么位置，我们所获得的距离都是正数。有趣吧，但是还不

够动态，在下面这个示例，可以实时地获得影片的距离，请试一下这个文档类

MouseDistance.as：
package {
 import flash.display.Sprite;
 import flash.events.MouseEvent;
 import flash.text.TextField;
 public class MouseDistance extends Sprite {
  private var sprite1:Sprite;
  private var textField:TextField;
  public function MouseDistance() {
   init();
  }
  private function init():void {
   sprite1 = new Sprite();
   addChild(sprite1);
   sprite1.graphics.beginFill(0x000000);
   sprite1.graphics.drawRect(-2, -2, 4, 4);
   sprite1.graphics.endFill();
   sprite1.x = stage.stageWidth / 2;
   sprite1.y = stage.stageHeight / 2;
   textField = new TextField();
   addChild(textField);
   stage.addEventListener(MouseEvent.MOUSE_MOVE, onMouseMove);
  }
  public function onMouseMove(event:MouseEvent):void {
   graphics.clear();
   graphics.lineStyle(1, 0, 1);
   graphics.moveTo(sprite1.x, sprite1.y);
   graphics.lineTo(mouseX, mouseY);
   var dx:Number = sprite1.x - mouseX;
   var dy:Number = sprite1.y - mouseY;
   var dist:Number = Math.sqrt(dx * dx + dy * dy);
   textField.text = dist.toString();
  }
 }
}

在这里dx和dx的值是用 sprite1 的位置减去当前鼠标位置得出的，dist的值放入一个文本框中进行显示，并在影片和鼠标之间绘制一条线(在下一章绘图API中会学到)。最后，将所有这些代码放到处理函数 onMouseMove 中，每次鼠标移动时进行刷新。测试一下这个文件，并移动鼠标，鼠标与影片剪辑之间会连接上一条线，并实时读取线的长度。

后面的章节中，在学到碰撞检测时，我们会发现内置的碰撞检测(hit testing)方法存在着先天不足，然后会看到使用勾股定理公式完成基于距离(distance-based)碰撞检测方法。它还非常适合用于计算重力或弹力等，因为这些力的大小与两个物体之间的距离成正比。

本章重要公式

现在我们已经有了一个全新的工具箱，同时又多了不少工具，全部所有的工具将会在第19章列出，那么让我们看看现在都有了哪些工具。注意，这些公式非常地抽象和简化，里面不包括数据类型和变量定义，在类中使用这些公式时，是否使用这些给出的句型取决于你。

基本三角函数的计算：
角的正弦值 = 对边 / 斜边
角的余弦值 = 邻边 / 斜边
角的正切值 = 对边 / 邻边

角度制与弧度制的相互转换：
弧度 = 角度 * Math.PI / 180
角度 = 弧度 * 180 / Math.PI

向鼠标旋转(或向某点旋转)：

// substitute mouseX, mouseY with the x, y point to rotate to
dx = mouseX - sprite.x;
dy = mouseY - sprite.y;
sprite.rotation = Math.atan2(dy, dx) * 180 / Math.PI;

创建波形：

// assign value to x, y or other property of sprite or movie clip,
// use as drawing coordinates, etc.
public function onEnterFrame(event:Event){
value = center + Math.sin(angle) * range;
angle += speed;
}

创建圆形：

// assign position to x and y of sprite or movie clip,
// use as drawing coordinates, etc.
public function onEnterFrame(event:Event){
xposition = centerX + Math.cos(angle) * radius;
yposition = centerY + Math.sin(angle) * radius;
angle += speed;
}

创建椭圆：

// assign position to x and y of sprite or movie clip,
// use as drawing coordinates, etc.
public function onEnterFrame(event:Event){
xposition = centerX + Math.cos(angle) * radiusX;
yposition = centerY + Math.sin(angle) * radiusY;
angle += speed;
}

计算两点间距离：

// points are x1, y1 and x2, y2
// can be sprite / movie clip positions, mouse coordinates, etc.
dx = x2 – x1;
dy = y2 – y1;
dist = Math.sqrt(dx*dx + dy*dy);

本文链接：http://www.blueidea.com/tech/multimedia/2008/5751.asp　

出处：蓝色理想
责任编辑：bluehearts

上一页 三角学应用 [8] 下一页

◎进入论坛RIA设计与应用版块参加讨论